Piaget的認知發展論,談到的兩種建構知識方式:
- 同化(assimilation):個體以既有的基模去吸收新經驗。
- 調適(accommodation):原有基模無法同化新知識時,個體只有改變已有的認知結構以符合環境要求。
現代教學設計,偏好讓學生用既有的知識學習新知識,讓他們用「同化」的方式學習
預設學生的先備知識是「三角形的內角和是180度」,
學習就是「用對角線把多邊形分割成數個三角形」,把三角形角度相加的體驗
古早時代,直接丟公式要學生背-不懂沒關係,給我背起來!也就是「調適」的方式
公式解:
多邊形內角和=(邊數-2)*180°
S=(N-2)*180°
接下來要分享的,是遇到思想比較奇葩的學生要怎麼辦
以前我的小學老師就跟我說「不能這樣切」
現在想想... 應該檢討他的能力不夠,不該怪我打斷教學
|
|
這是一個三角形,內角和是180°
如果不知道幾度怎麼辦?
1.從考卷撕下一個三角形,把三個角拼起來
2.拿出90° - 45° - 45°三角板,把三個數字加總
3.使用畢氏定理證明它(聽起來很厲害)
|
 |
那麼,什麼是四邊形? 四邊形是一個形狀,它有四個邊 |
所以我們想求四邊形的內角和 為什麼不叫它四角形? 說的好,它有四個角-也叫四角形 就和番薯和地瓜一樣,名稱是通用的,我們不會特別糾正別人的說法 |
|
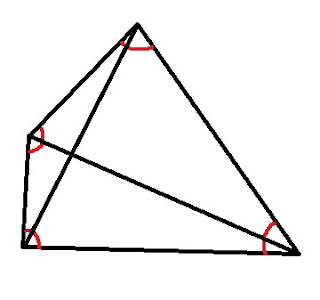
「用對角線把它切成三角形」解一 所以是 180° + 180° = 360° |
|
「用對角線把它切成三角形」解二 180° + 180°+ 180°+ 180° = 720° 中間那四個角多算了 那四個角剛好360° ,要扣回來 720°- 360° = 360° |
「用對角線把它切成三角形」解一 所以是 180° + 180° + 180° = 540° |
|
「用對角線把它切成三角形」解二 困難點不是出在三角形太多, 而是中間那個該死的五邊形---只能切成三個三角形了吧? 有點洩氣呢....不過還是把它算完 180° *13 - 360°*5 = 540° |
[圖:小學生嘗試用奇葩式解法求六角形內角和]
(此為對於多邊形「內角」的迷思與意義不清楚所致)
這張圖原自 http://163.19.142.4/wordpress/?p=351 ,原網頁已經不見了
奇葩式切法的經驗整理:
六邊形可以切六塊,減掉中間的360°
七邊形沒辦法,中間是七邊形-----狀況和五邊形一樣
......
......
為什麼不繼續研究下去直到找出規律呢?
因為~十邊形已經切成這樣了!
一個多邊形,有很多個角
我們尋找由繁化減的方法來求它的內角和
以這張圖來看,
十邊形內部的形狀,沒有一個是大於十邊的,代表著「可以從已知來求未知」的可能性
貝卡:「我的手好痠」
「繞了很多遠路之後,我才發現大家為什麼要往那裡走」
小學時除了凸多邊形的學習,我也曾經想探討凹多邊形的內角和
結果因為能力不足,支持不夠多...
總之失敗了~_~
|
|
多邊形內角和=(邊數-2)*180°
如何證明凹凸多邊形都適用這個結論?
1.找出凹邊形的三角化方法(證明分割法適用於任何凹多邊形)
2.觀察規則
凹四邊形:凸三邊形一邊內凹
凹五邊形:凸三邊形二邊內凹;凸四邊形一邊內凹
凹六邊形:凸三邊形三邊內凹;凸四邊形二邊內凹;凸五邊形一邊內凹
凹七邊形:凸四邊形三邊內凹;凸五邊形二邊內凹;凸六邊形一邊內凹
凹八邊形:凸四邊形四邊內凹;凸五邊形三邊內凹;凸六邊形二邊內凹;凸七邊形一邊內凹
只想偷看答案,一點都不想研究咧?
google「凹凸多邊形內角和」
結論是相等!
|